Neural Turing Machines

08 May 2017 | PR12, Paper, Machine Learning, Neural Turing Machine

오늘 소개하려는 논문은 역시 Google DeepMind의 “Neural Turing Machines”라는 - 제목부터 범상치 않은 - 2014년 논문입니다.

Neural Turing Machine의 개념

Neural Turing Machine을 한 마디로 정리하면, 외부의 메모리에 연결할 수 있는 neural network입니다. Neural network와 외부 메모리가 결합된 시스템은 Turing Machine과 일부 유사한 특징을 가집니다.

사실 컴퓨터공학을 전공해도 Turing Machine에 대해 깊게 알아볼 기회는 많지 않습니다. 네이버에서 튜링 머신 [Turing machine]을 찾아보면 다음과 같은 설명이 나옵니다.

1936년에 Turing이 고안한 추상적 계산 기계. 튜링 머신은 순서에 따라 계산이나 논리 조작을 행하는 장치로, 적절한 기억 장소와 알고리즘만 주어진다면 어떠한 계산이라도 가능함을 보여 주어 현대 컴퓨터의 원형을 제시하였다. – 튜링 머신 [Turing machine] (실험심리학용어사전, 2008., 시그마프레스㈜)

튜링 머신은 아래 그림과 같이 알고리즘(program)대로 현재 state와 tape에서 읽은 기호에 따라 다음 state를 결정하고, read/write head가 tape의 칸에 기호를 쓰고, read/write head를 좌우로 한 칸 움직이는 동작을 조합해서 실행합니다.

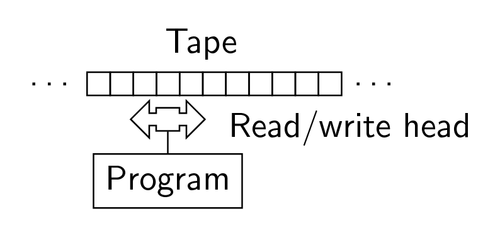
폰 노이만 아키텍처 (Von Neumann architecture)와 비교하자면, 튜링 머신은 기계를 사용해 수학적인 문제를 사람처럼 풀기 위한 이론적인 개념이고 폰 노이만 아키텍처는 튜링 머신의 개념을 바탕으로 실제 컴퓨터를 구현하기 위한 구조라고 할 수 있습니다.

Neural Turing Machine을 제안하는 이유가 뭘까요? 그것은 미분 가능한(differentiable) 컴퓨터를 만들 수 있기 때문입니다.

수학의 정석에도 나오듯이 미분 가능하려면 먼저 continuous해야 합니다. 그런데 Turing machine을 비롯해서 우리가 잘 알고 있는 디지털 컴퓨터는 기본 operation들이 discrete합니다. 즉, 0아니면 1, 여기 아니면 저기로 딱딱 끊어집니다.

예를 들어, 10이라는 값이 들어 있는 1000번지에서 읽으면 10이 그대로 읽힙니다. 999번지나 1001번지의 값에 영향을 받지 않습니다. 1000번지에 20이라는 값을 쓴다면 1000번지에만 20이 쓰여지지 999번지나 1001번지의 값이 그에 따라 달라지는 일은 없습니다. 뒤에서 다시 설명하겠지만 Neural Turing Machine은 이런 기본적인 operation들을 실수(real number) matrix 연산으로 바꿔 continuous하고 미분 가능하게 만듭니다.

미분 가능하면 뭐가 좋을까요? Gradient descent를 사용하는 다양한 최적화 알고리즘을 적용할 수 있습니다. 이 논문에서처럼 Neural network를 사용하면 back propagation으로 쉽게 training할 수 있다는 장점이 생깁니다. (아래 그림은 Daniel Shank의 슬라이드에서 일부 인용했습니다.)

Neural Turing Machine의 구조

먼저 가장 기초적인 Neural Network의 개념은, external input을 받아 external output을 만드는 아래 그림처럼 단순한 구조로 생각할 수 있습니다. 바로 다음에 설명할 RNN과 비교해 feedforward neural network이라고 부르기도 합니다. (아래 그림은 Kato Yuzuru의 슬라이드에서 일부 인용했습니다.)

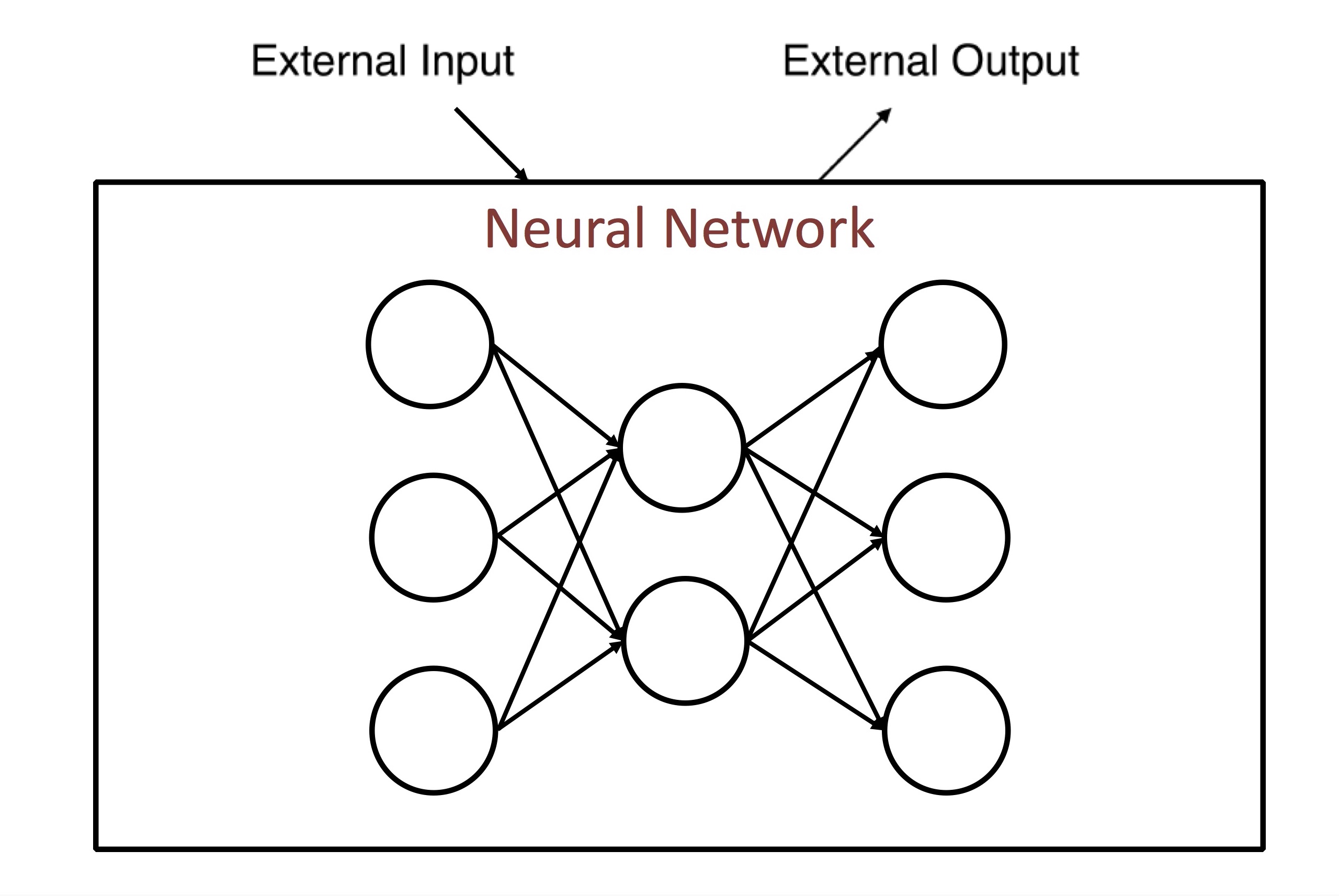
여기서 발전된 RNN (Recurrent Neural Network)은 unit 자체의 출력을 다시 입력으로 받는 directed circle을 도입해서 일종의 internal memory 개념을 구현했습니다. 즉, RNN의 current state는 external input과 previous state로부터 결정이 됩니다.

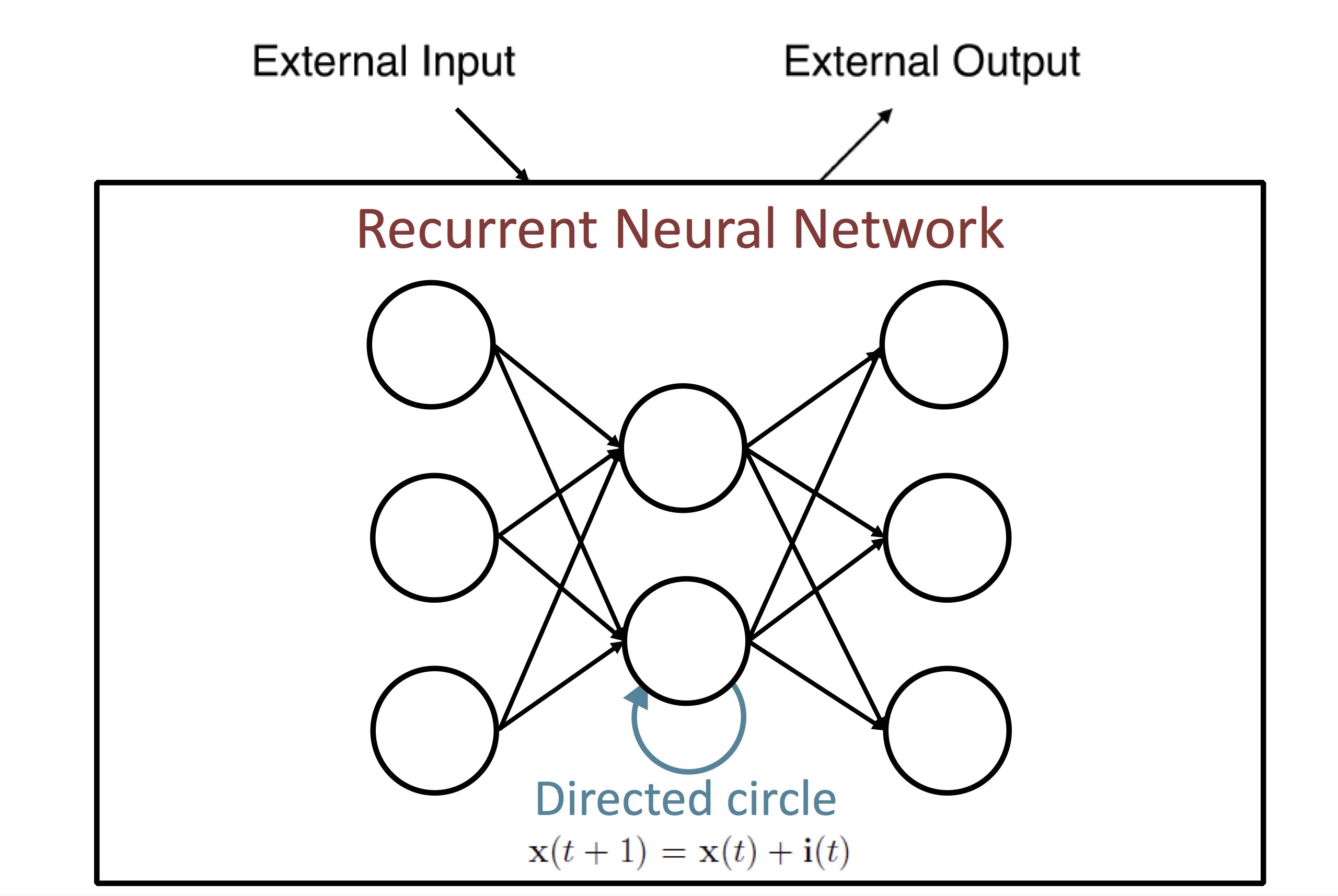
반면, Neural Turing Machine은 external memory를 사용할 수 있는 구조입니다. 이 논문에서 controller라고 부르는 부분이 neural network입니다. Controller는 read head와 write head를 통해 memory에 읽고 쓸 수 있습니다. 여기서 ‘head’는 memory I/O operation을 추상화한 개념입니다. Turing machine에서 tape를 읽고 쓰는 부분의 용어를 그대로 사용해서 오히려 약간 혼란스럽게 느껴지기도 합니다.

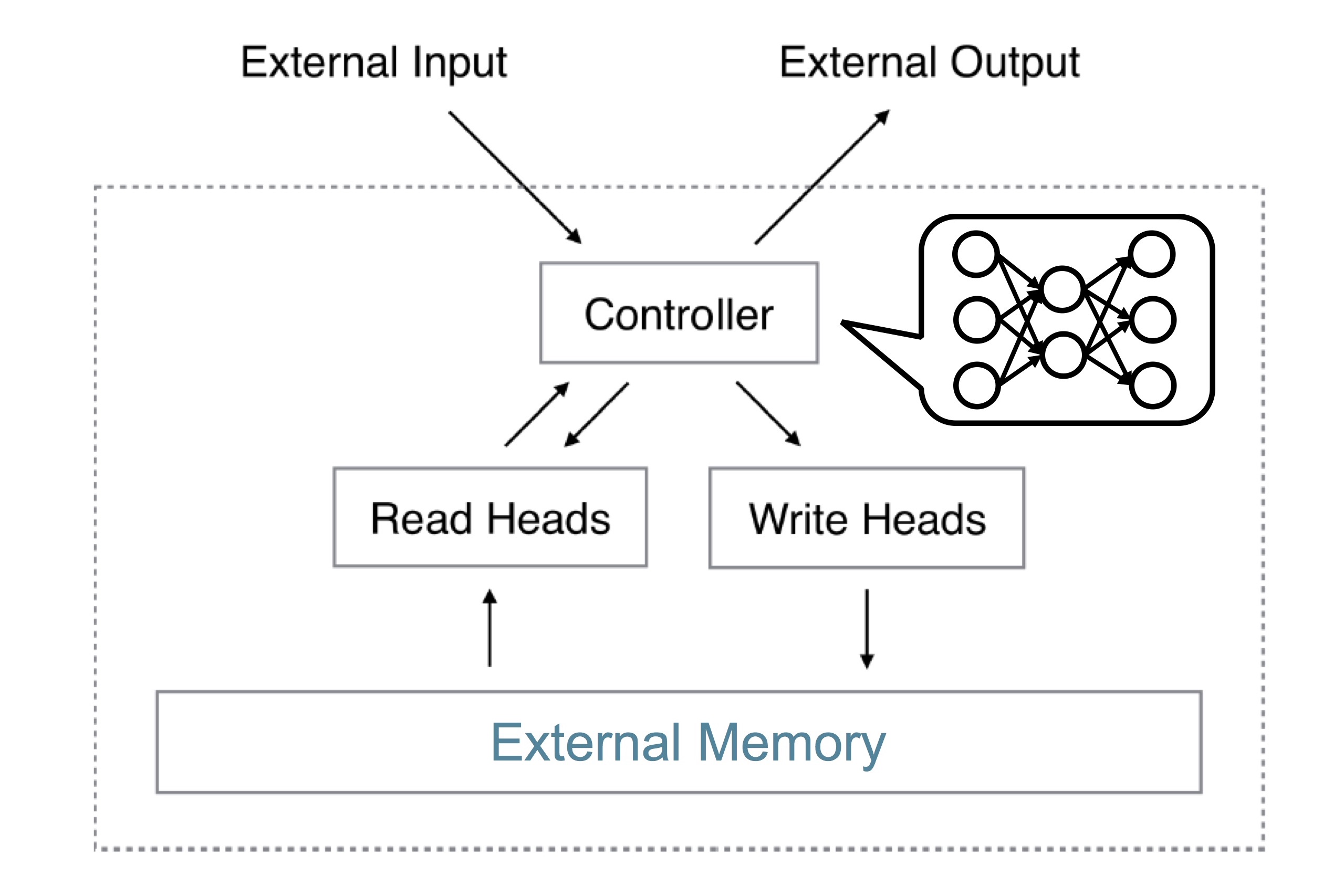
Neural Turing Machine의 구현

아래 그림은 메모리에서 데이터를 읽고 쓰는 전체 구조를 한눈에 보입니다.

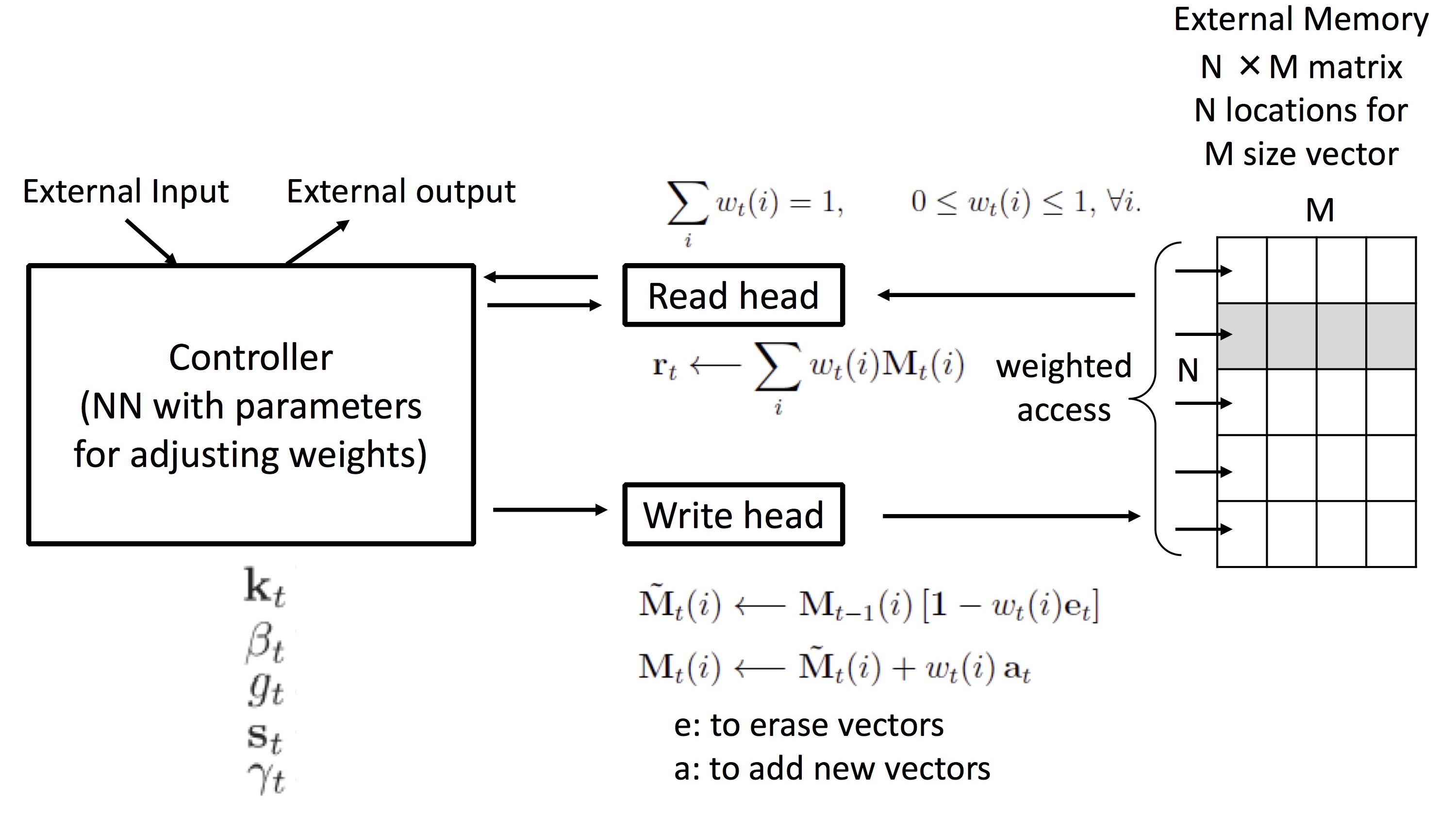
이 그림의 Read head라는 부분에서 실행하는 메모리 읽기 연산은 (1)식과 같습니다. 어느 번지 하나에서 바로 읽어오는 것이 아니라 $N$개의 번지에서 읽어 weight vector $w_t(i)$와 linear combination한 값을 읽어 옵니다. 즉 주변 값들의 영향을 받게 되는데 논문에서는 이를 ‘blurry’하다고 표현합니다. weight $w_t(i)$는 0과 1 사이의 값을 갖는 real number vector이며 계산 결과 읽는 값 $\mathbf{r}_t$도 real number vector가 됩니다.

$$\begin{align} \tag{1} \mathbf{r}_t \leftarrow \sum\limits_i^R w_t(i) \mathbf{M}_t(i) \end{align}$$

Write head에서 실행되는 쓰기 연산은 (2), (3)식과 같이 삭제(erase) 후 덧셈(add)하는 2개의 식으로 구현됩니다. 마찬가지로 쓰기도 linear combination하면서 주변 값들의 영향을 받아 blurry한 특성을 가집니다. 중요한 것은 읽기, 쓰기가 모두 matrix 연산으로 구현되므로 미분 가능하다는 점입니다.

$$\begin{align} \tag{2} \tilde {\mathbf{M}}_t(i) \leftarrow \mathbf{M}_{t-1}(i)[\mathbf{1} - w_t(i) \mathbf{e}_t ] \end{align}$$ $$\begin{align} \tag{3} \mathbf{M}_t(i) \leftarrow \tilde {\mathbf{M}}_t(i) + w_t(i) \mathbf{a}_t \end{align}$$

메모리의 주소를 계산하는 addressing mechanism을 아래 그림에 보입니다. 이 논문이 제안한 모델에서 메모리 주소를 계산하는 것은 weight vector $w_t(i)$를 결정하는 것과 같습니다.

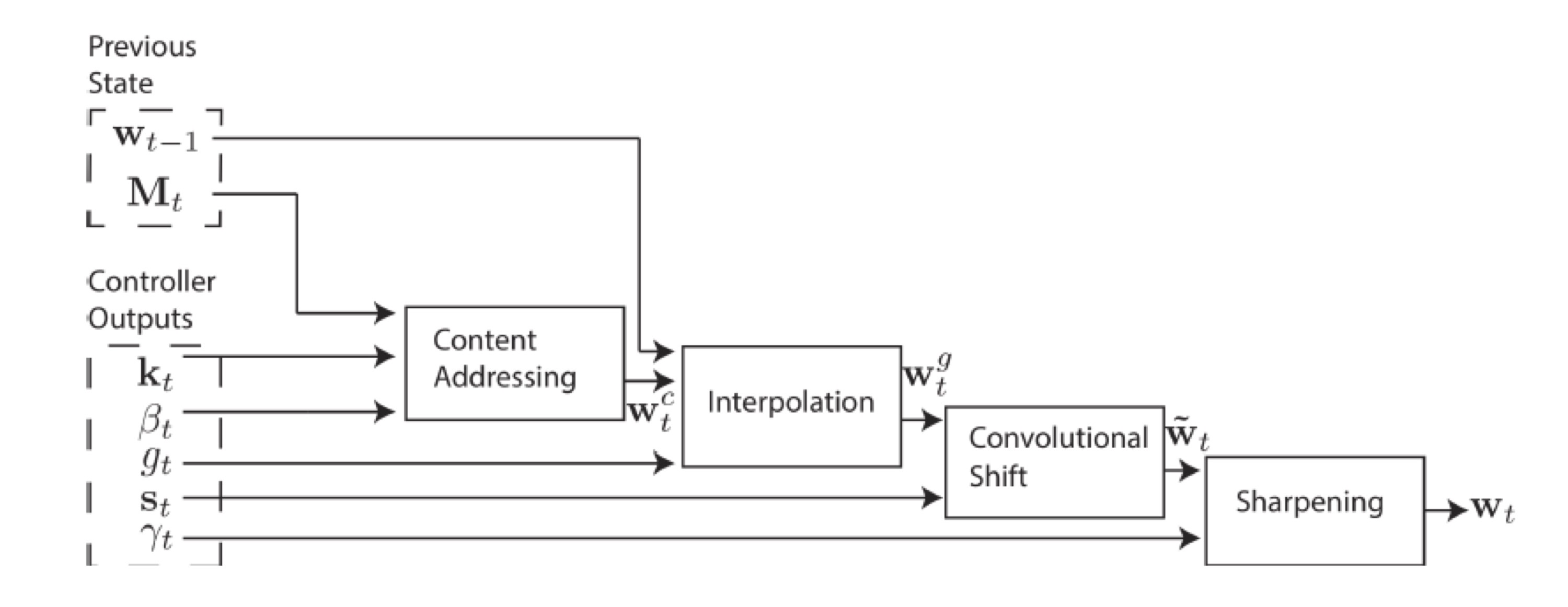
이 논문에서 제시된 addressing 방법은 두 가지가 있습니다. 하나는 주어진 key vector 값과 유사한 정도를 계산해 찾는 content-based addressing이고, 다른 하나는 location에 따라 찾는 location-based addressing입니다.

전체 addressing mechanism은 4단계로 복잡하게 이뤄지는데 간략히 요점만 설명하면 다음과 같습니다.

1. Content Addressing: key vector $\mathbf{k}_t$ 와 비슷한 정도를 cosine similarity로 평가해서 content-based weight $\mathbf{w}_t^c$를 계산합니다.
2. Interpolation: $\mathbf{w}_t^c$ 값과 이전 state $\mathbf{w}_{t-1}$의 값을 가중치 합산해서 $\mathbf{w}_t^g$를 구합니다.
3. Convolutional Shift: head 위치를 앞뒤로 shift하는 것을 convolution으로 계산해 $\tilde {\mathbf{w}}_t$를 얻습니다.
4. Sharpening: $\tilde {\mathbf{w}}_t$을 scaling하여 ${\mathbf{w}}_t$를 계산합니다.

실험 결과

이 논문에서는 Copy, Repeat Copy, Associative recall, Dynamic N-Grams (N개의 이전 bit에서 다음 bit 예측), Priority Sort에 대해 실험했습니다. 비교 대상으로는 feedforward neural network controller의 NTM, RNN LSTM controller의 NTM, (NTM 아닌) RNN LSTM을 사용했습니다. 모든 실험의 학습에 RMSProp 알고리즘에 Momentum 0.9를 적용했고, 모든 LSTM은 3개의 hidden layer를 가지고 있습니다.

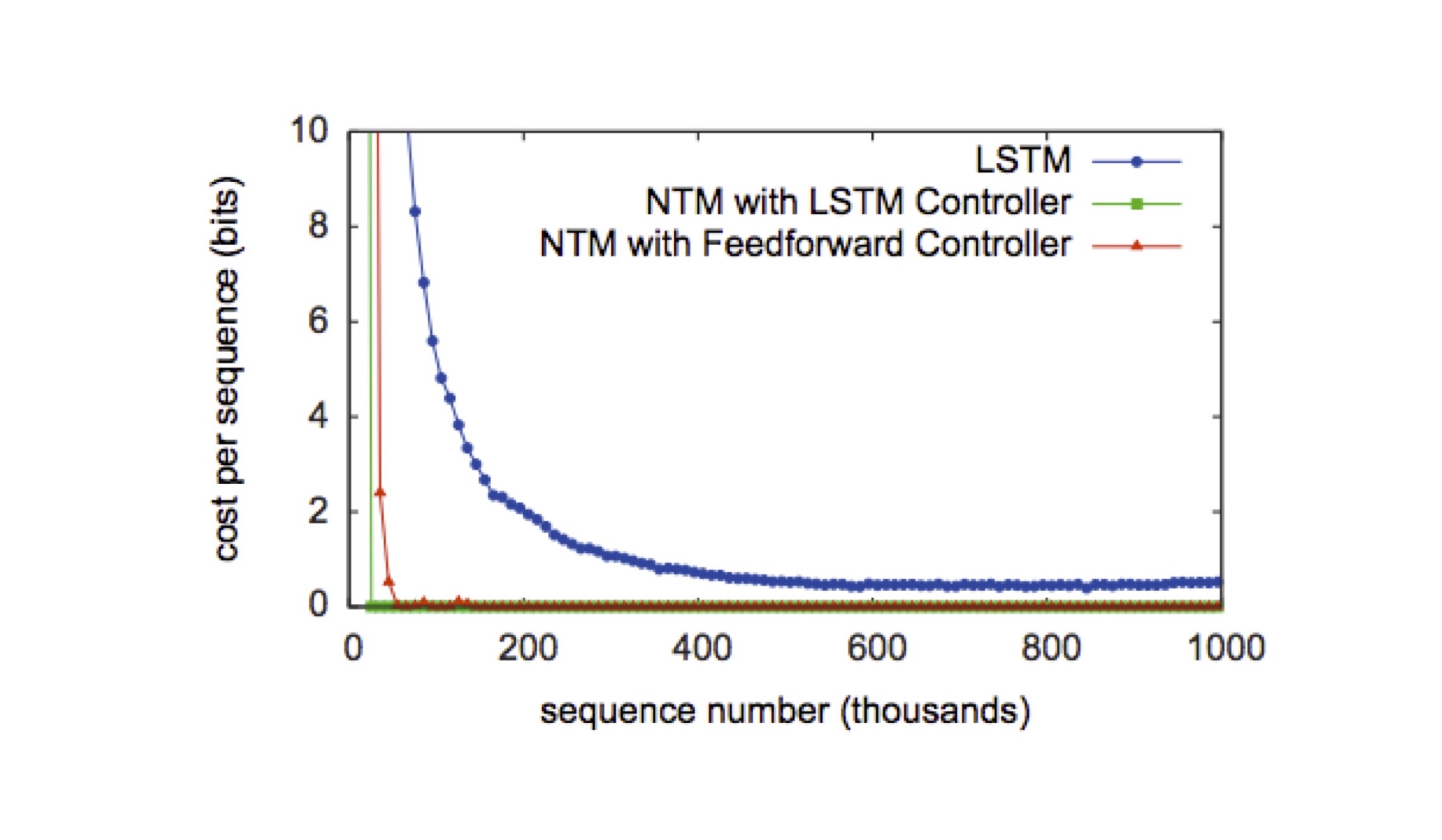
아래 그림은 Copy 실험의 결과입니다. 그래프에서 NTM을 적용한 2가지 경우가 LSTM만 단독 적용한 경우보다 훨씬 학습이 빠른 것을 볼 수 있습니다.

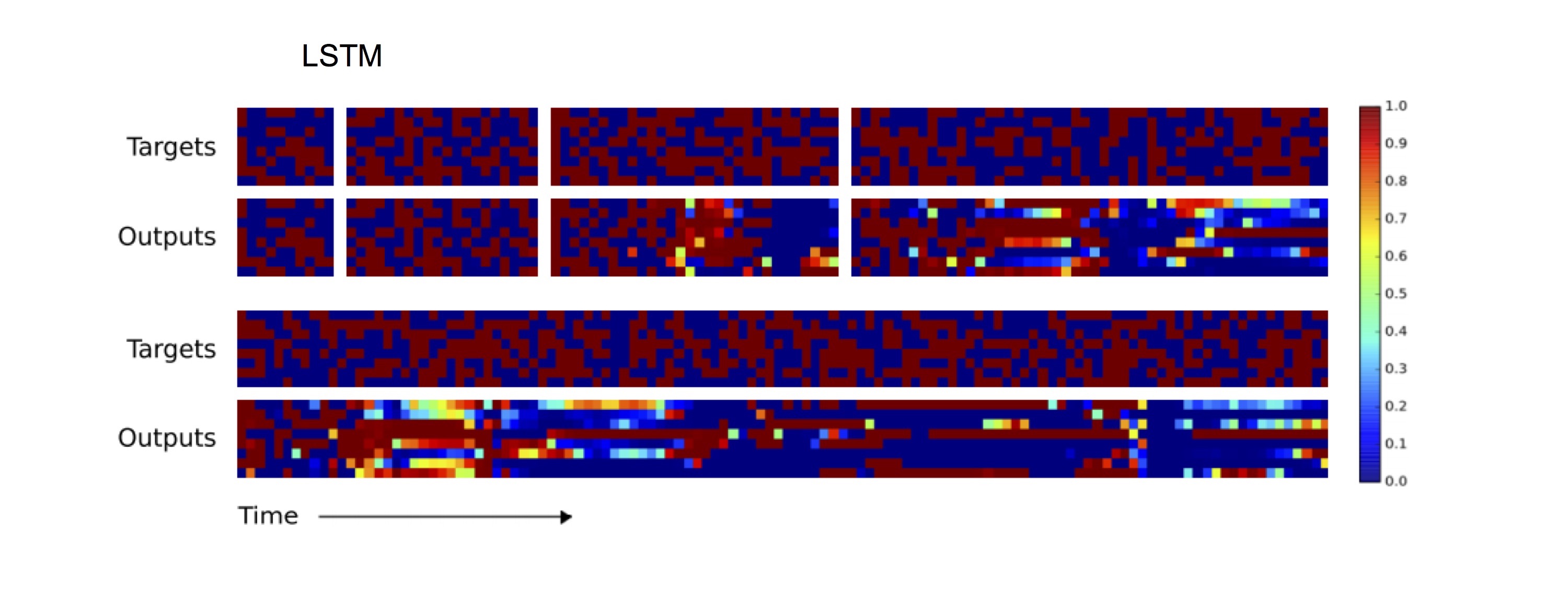
아래 그래프의 위쪽 2개의 row는 NTM에게 길이가 10, 20, 30, 50인 test 입력을 copy하도록 한 것입니다. 아래쪽 2개의 row는 길이가 120인 경우입니다. NTM에게 길이가 20인 copy를 train했음에도 오류가 매우 적은 것을 볼 수 있습니다.

반면, LSTM의 경우에는 길이 20까지는 오류가 거의 없지만 그 이상이 되면 급격히 오류가 많아지는 것을 관찰할 수 있습니다.

요약하면, NTM은 copy, sort와 같은 단순한 알고리즘을 매우 효율적으로 학습하고 training 범위를 벗어난 문제에 대해서도 높은 성능을 내는 것을 알 수 있습니다.

후속 연구

이 논문의 저자들은 이 모델을 발전시켜 2016년 Nature에 “Hybrid computing using a neural network with dynamic external memory”라는 논문을 게재했습니다. 이 논문은 NTM의 3가지 제약점을 개선한 Differential Neural Computer (DNC)라는 새로운 모델을 제시했습니다. 개선점 3가지는 아래와 같습니다.

1. 할당된 memory block들이 서로 겹치거나 방해가 되지 않도록 보장
2. 사용된 memory를 free해서 reuse할 수 있게 함
3. temporal link라는 개념을 도입해서 연속적이지 않은(non-contiguous) 메모리 접근 시 문제 해결

아래 그림은 Nature에 실린 DNC의 아키텍처입니다.

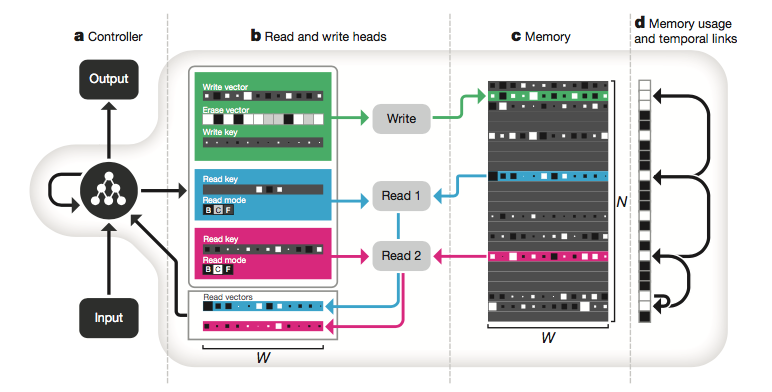
이 논문의 더 상세한 리뷰는 나중에 새로운 포스트로 추가하겠습니다.

– Jamie;

References

• Alex Graves의 paper @arXiv.org
• the morning paper 블로그의 논문 요약
• Daniel Shank의 슬라이드 “Neural Turing Machines: Perils and Promise”
• Daniel Shank의 발표 “Neural Turing Machines: Perils and Promise”
• Kato Yuzuru의 슬라이드 “A summary of Neural Turing Machines (NTM)”
• Ilya Kuzovkin의 슬라이드 “Neural Turing Machines by Google DeepMind”
• 서기호 님의 동영상 “PR-006: Neural Turing Machine”
• Alex Graves의 인터뷰 (Linkedin) “Deep Minds: An Interview with Google’s Alex Graves & Koray Kavukcuoglu”
• Wikipedia의 Neural Turing Machine
• Mike James의 article (IProgrammer) “DeepMind’s Differentiable Neural Network Thinks Deeply”
• Wikipedia의 Turing Machine
• Alex Graves의 “Hybrid computing using a neural network with dynamic external memory”